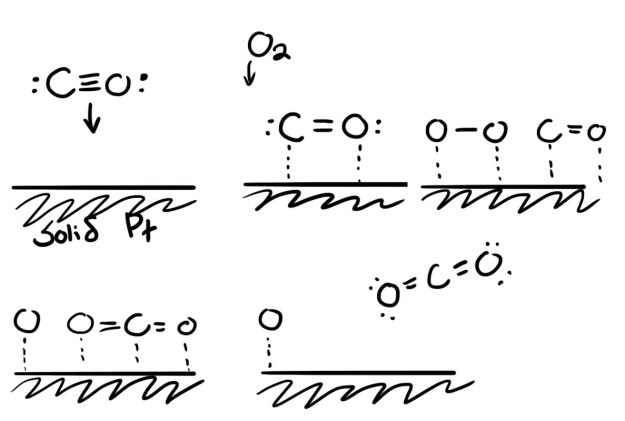Category Archives: Science

Fun Science: Why’s platinum so special?

2 Replies

In science, we tend only to learn about a small subset of the elements that populate our world. This is not unreasonable, since 96% of our bodies are composed of just hydrogen, water, carbon, and nitrogen. But there are over a hundred more elements, and they often influence life outside our bodies in ways we don’t hear about. So in today’s post I will talk about platinum.

Platinum is one of the rarest metals in the Earth’s crust. Only 192 tonnes of it are mined annually, where 2700 tonnes of gold are mined annually. When the economy is doing well, platinum can be twice as expensive as gold. So what’s so valuable about it?

Platinum is used a lot in jewelry. Platinum has the appearance of silver, but it doesn’t oxidize and become tarnished like silver. It’s harder than gold, and its rarity can be appealing.

But it’s the chemical properties of platinum that set it apart. Platinum is a great catalyst. This means that platinum facilitates chemical reactions, but is not consumed as the reaction proceeds. The catalytic converter in your car is a platinum catalyst. The catalytic converter helps eliminate a variety of undesirable compounds such as carbon monoxide, nitrous oxides, and incompletely combusted hydrocarbons. Platinum is also a critical part of current hydrogen fuel cells; it splits hydrogen into protons and electrons.

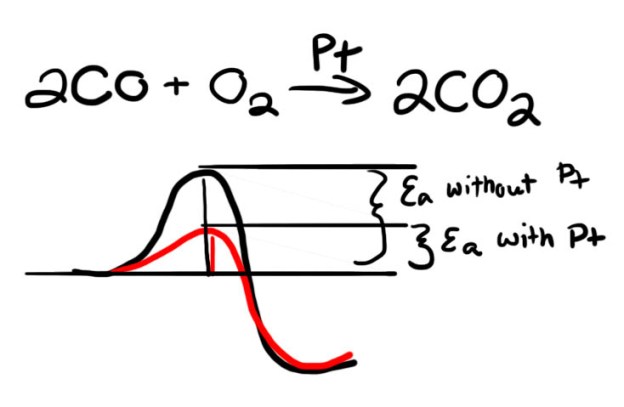
Platinum doesn’t force reactions to occur, but it makes them easier by reducing the energy required. The image below shows the reaction of carbon monoxide (CO) to carbon dioxide (CO2). The chart at the bottom shows the potential energy before, during and after the reaction. Imagine a ball rolling along the red curve (with platinum) and the black curve (without platinum). The ball on the black curve will need more speed to get over the hump. Any given ball is more likely to get over the red hump. Likewise, the presence of platinum lets CO get over the hump to become CO2. Platinum does this for all kinds of reactions.

activation energy

The reaction takes less energy because once a molecule bonds to the surface of platinum, the bonds within the molecule are a little weaker. Molecules like O-O and H-H can split into singletons, something they would never do off the surface. Below I show an example reaction for CO to CO2 on platinum. This diagram is meant to be illustrative, a possible mechanism for the reaction and to show how platinum helps out. In reality these reactions occur very quickly, and careers can be spent figuring out exact reaction mechanisms.

catalysis

 

Platinum is a bit like velcro. Molecules become hooked to the surface, do their reaction, and unstick. If molecules stick and then refuse to unstick, this is called catalyst poisoning, and it’s a big issue in fuel cells. Like velcro, once the hooks are occupied, they can’t do anything else. Platinum is a good catalyst because a lot of things (like hydrocarbons) want to stick to it, but they don’t stick too hard. Other metals either are not attractive enough, or they are too attractive. Platinum is so valuable because, besides being rare, its properties happen to be balanced just right for the reactions we want.

 

Fun Science: Crystals Everywhere!

2 Replies

I went on a trip to DC last fall. Almost accidentally I ended up in the Natural History Smithsonian Museum. Wow! Especially worthy is the section on minerals. I assume there are other museums with such displays, but I hadn’t been to one. The Hope diamond is displayed also in the minerals section, but fancy jewels I can’t touch are way less interesting than all the minerals and natural crystals.

I find crystals fascinating because they tell you so much about the microscopic structure of the material. Where else in life can you just look at an object and see what it does down to the nanometer? So naturally the camera came out. Below are a few favorites, and some comments about what we can infer from the pictures.

IMG_2197

Fluorite (CaF2): As you can see, Fluorite has a cubic crystalline structure. Fluorite can come in basically any color. Color can be due to impurities, exposure to radiation, or defects in the crystalline structure. Fluorite was originally so named due to fluorescent properties; fluorite can fluoresce in a variety of colors depending upon the impurities present.

IMG_2139Beryl (Be3Al2(SiO3)6): You might be more familiar with other names for Beryl, such as aquamarine or emerald or morganite. Beryl is naturally clear, but takes on color in the presence of impurities. Emerald, for example, has chromium or vanadium present. Aquamarine coloration results when the Fe2+ oxidation state is present. Fe3+ results in yellow coloration. You can see in the image above that beryl has a hexagonal crystal structure. You can also see that this is one big hexagonal crystal, unlike the population of cubes in the fluorite picture. This tells us a lot about how the crystal grew. If the crystal grew very fast, there would be a number of columns, because crystallization would be faster than the time for the mineral components to diffuse to one specific column. So this crystal grew pretty slowly.

IMG_2136

 

Wulfenite (PbMoO4): Wulfenite is often found around lead deposits, which makes sense since it contains lead. It has a tetragonal crystal structure, and tends to be yellow or orange or brown in color. You can see that the crystals are much smaller in this picture than the beryl crystal. Clearly these crystals grew quickly from many nucleation sites. The size to which crystals tend to grow is a property of the crystal too; some only form a ton of small crystals, some form a few very large ones. It depends whether it is lower energy to just form another crystal, or if it is lower energy to allow diffusion to an already established crystal. This is related to thermodynamics. Wulfenite seems to favor lots of small crystals. Some wulfenite has a really cool property called piezoelectricity; when there is the right kind of pressure on the crystal, an electric charge accumulates.

IMG_2219

 

Manganese dioxide (MnO2): This manganese dioxide has grown in a dendritic fashion. It might look like frost or snowflakes, which grow in similar ways. These dendrites are very fractal, a favorite topic of mine. Here diffusion was definitely limited, so crystals grew where the materials were present.

IMG_2174

 

Chalcedony (SiO2): Chalcedony is a type of silicon dioxide, which is the chemical composition of most sand. Chalcedony is composed of two different silicon dioxide minerals: quartz and moganite. Quartz and moganite have different crystalline structures which grow together at a fine scale in chalcedony, which is probably why it looks far less geometric than the other crystals I’ve shown. Agate is a type of chalcedony.

 

Fun science: scale-free networks

Leave a reply

A scale-free network is a network with self-similar structure. As you zoom in on parts of the network, the sub-network resembles the overall network. In this way, scale-free networks are the network analogy of fractals. (Read previous posts about fractals, or fractals in nature.) Fractals arise in many natural systems like coastlines, snowflakes, and topology; likewise many naturally arising networks are self-similar. Examples include links on the internet, social networks, and protein interaction networks. Understanding the structure of a network helps us to understand the types of behavior that can occur on the network. Some network structures are more prone to failure or instability, or different types of failure or instability.

Scale-free networks have a sort of hub arrangement. Some elements connect to a bunch of other elements, while most connect to just a few. Going back to the social network analogy, the hubs are those people with 1500 friends on Facebook, while most people have 100 or so. In the picture below, a random network is shown on the left, and a scale-free network is shown on the right (hubs shown in grey). In the random network, all the elements have roughly the same number of connections, with some slightly more, some slightly less. The scale-free there has more variation in number of connections amongst elements.

From Wikipedia page on scale-free networks.

Getting more mathematical, the number of connections an element has gives its degree. An element with 3 connections has a degree of 3. We can say, hypothetically, that element 1 has a degree of 2, element 2 has a degree of 6, element 3 has a degree of 2, etc. We have degrees for all of the elements of the network. If we organize this set of degrees into a histogram (where we bin by degree value– in our example, we had counted two of degree 2, and one of degree 6) we get a degree distribution.

If something is distributed normally, the histogram has a bell-shape to it, like the first picture below. If you did a histogram of the height of all the people in your city, it would be a normal distribution. If it is distributed in a scale-free fashion, there are a few high value elements (high degree in our case), and a lot of low value elements. This gives the bottom picture, with a peak at a low value and a long tail into the higher values. The wealth distribution in your city probably looks like the scale-free distribution. If you take the log of the values on the scale-free distribution, you will get a straight line. This is because the logarithm is the inverse of the function 10^x; if you take the log of something, you can see its behavior on the 10^x scale, which gives you insight into how it behaves across multiple powers of 10, or its “scaling free” behavior.

From Wikipedia article on normal distribution

From Wikipedia article on power-law distribution

If you are interested in other basic explanations of more advanced science, also check out my posts on synchrony, chaos, network theory, and small-world networks.

Americans are (statistically!) Weird

Leave a reply

Have you ever wondered how social scientists conduct their psychological experiments? They mostly use volunteer American college undergraduates. This might seem obviously flawed; can a bunch of educated 20-year-olds possibly even represent the American spectrum, much less the world? The field hypothesized that the human brain structure is universal, and thus reasoning and decision-making as a consequence of that structure should be universal. The article “Why Americans are the Weirdest People in the World” explores the research of Joe Henrich. The article discusses how different cultures solve different problems, and how truly diverse thinking processes are across the globe. And wouldn’t you know it, Americans are crazy, crazy outliers in all of the problems.

Economics often uses behavioral experiments of game theory to understand choices that people make. In the famous “prisoner’s dilemma”, two “prisoners” may choose whether or not to rat out the other prisoner. Depending upon the choices of the two, there are four possible outcomes. If both betray, they are collectively worst off (say two years of prison each). If A betrays B and B does not betray A, A goes free while B gets 3 years of prison, and likewise for the reverse. If neither betray, they are collectively best off, and get a year each. The constructs of the game reward deceit.

Joe Henrich played such games with natives in Peru. The Ultimatum game is a version of the prisoner’s dilemma. Player 1 is given $100. He must make an offer to player 2. If player 2 feels the offer is too low, he may reject it, in which case both players keep nothing. Both players know the rules. Player 1 is compelled to offer enough so that player 2 does not feel cheated. In the US, the offer is typically close to $50, and lower offers are typically rejected. In Peru, the offer was much lower, and it was typically accepted. The people in Peru figured money was money, why reject it? Different cultures displayed different reactions to the Ultimatum game yet. The US is relatively typical of the west in this game. The researchers supposed that in a western society, people have grown to accept some inconvenience on their own behalf to punish dishonesty or greed, such as taking the time to write a complaint to the Better Business Bureau.

The article goes on to detail that Americans are outliers statistically. This has major implications for economics and sociology and psychology. It’s a great read, and for my part, I think a reason to take these kinds of sciences with a grain of salt. They are definitely fields worthy of study, but definitive conclusions are difficult. We know most that we know little about the human brain. Even if you aren’t particularly interested in the science, the article is a fascinating read just for the variety of human thinking.

Fun Science: Small World Networks

1 Reply

The small-world phenomenon refers to the fact that even in a very large population, it takes relatively few connections to go from any element 1 to another random element. Amongst people, we know this concept as the “six degrees of separation” game. Any population of objects with connections can be conceptualized this way. Examples include crickets communicating by audible chirps, websites with links, electrical elements with wiring, board members with common members, or authors on mutual scientific papers. All of the examples I list have been examined in various scientific studies.

In a small-world network, elements are first connected in a regular lattice; for example, each element is connected to one or two nearby neighbors on each side. The leftmost picture below shows a regular lattice of elements. A connection between element i and element j is then removed. Then we add a connection between element i and any other element x, like the middle picture below. If x is across the network from i, then the number of steps between i and x has been reduced from some large number to 1. All of the elements connected to i are now 2 steps from element x. This reduces the diameter of the network, which is the maximum number of steps between any two elements, although the number of connections remains constant. In the six-degrees of separation game, the diameter would be 6. As we replace more of the lattice connections with random ones, the network becomes more and more random. We quantify a small-world network by its randomness, as in the picture below.

The small-world network has been explored as a means of sending information efficiently through a population. As the diameter reduces, the time it takes information to spread through the entire network reduces. Neurons in the brain have been explored as small-world networks; certain regions of the brain are highly interconnected with a few long distance connections to other regions of the brain. Protein networks and gene transcription networks have also been described with the small-world model. Further information with scholarly references is available on the scholarpedia page (which is generally a great resource for complex systems problems).

 

Here you can read a good scientific paper by Steven Strogatz, one of the premier scientists in the area. This is a paper published in Nature, one of the highest scientific publications. There are some equations, but the figures are also excellent if you are uncomfortable with the math. The paper models the power grid, boards of directors, and coauthorship using network ideas. I mention this paper specifically because I find Strogatz a very relatable and clear writer. Also consider reading his recent nontechnical book about math, The Joy of X, for more math fun.

Check out my other science posts on graph theory, chaos, fractals, the mandelbrot set, and synchrony. And drop a note with any questions!

Beautiful Books: “Radioactive: Marie & Pierre Curie”

1 Reply

I first saw “Radioactive: Marie & Pierre Curie: A Tale of Love and Fallout” in an expat bookstore in Belgium. The book is vibrant and colorful and intriguing. After I got back, the book was still on my mind, and I purchased it. The book is an art-collage biography of Marie and Pierre Curie, and their Nobel-prize winning work on radiation. Their work is so influential that they named several elements (radium and polonium). A unit of radioactivity, a Curie, bears their name, and the element Curium was named for them.

Every page of this book is truly beautiful. The colors are deep and wonderful. Somewhere in the book, the author describes the techniques she used, and how they were specifically inspired by radioactivity, but I have not found this description on the web. This book is much more beautiful than most graphic novels, and I love that it is about science. The book makes Marie Curie especially relatable. She’s still the most famous female scientist a century after her great discoveries. She comes across as driven but human.

Here, then, is the big caveat in my review. The author relates a mostly negative view of radioactivity and nuclear advances. The damage to Marie and Pierre’s bodies, as well as their daughter, is given in detail. The bombing of Japan, the three-mile island incident, and Chernobyl are covered in great detail.

I found it incredibly saddening reading about Marie Curie, the most recognized female scientist perhaps ever, and then to read essentially a condemnation of the outcomes of her work. I also think this condemnation was unfair. To write the story of coal or gasoline would be to include tales of mesothelioma, ground water pollution, and air pollution bad enough in many parts of the century as to blot out the sun. The motors of wind power require mining for difficult-to-acquire materials, which comes from messy mining. No form of power comes without its evils just yet. That’s why we have scientists like the Curies, to keep stabbing away at the problem. Nuclear energy frightens people more than other forms of energy, but I think this is mostly an irrational fear. A simple Geiger counter reveals any stray radiation. Do you know when there are trace amounts of benzene about (a common hydrocarbon in oil)? Or other carcinogens? Hundreds of Superfund sites exist across the USA, many of them from hydrocarbon contamination. These sites can take decades to remediate.

Nonetheless, this book is beautiful and worth reading. The writing about Marie and Pierre Curie as people was wonderful. For those unfamiliar with the science of radioactivity, perhaps it will be a more inspiring read than it was for me.

Fun Science: Network Theory and Graphs

3 Replies

If you have a set of items and you can connect or sequence them in many ways, you probably have a graph or network. Clearly if you have these objects, some connection arrangements might be preferable to others. Heart cells are connected in patterns that contract the heart in the proper pattern. If you must deliver items to ten different locations, different paths may be more efficient (the traveling salesman problem).

Euler’s 1735 Koenigsberg bridge problem is considered the first graph theory problem. At the time, the city of Koenigsberg had seven bridges (shown above). Euler wished to find a path which crossed each bridge exactly once. He showed mathematically that no path satisfied those constraints.

The famous game “six degrees of Kevin Bacon” is a network theory problem. This game says that with six steps, any actor can be linked to Kevin Bacon through films pairs of actors appeared in. This idea was originally introduced at the Erdös number. Paul Erdös was a brilliant and highly published mathematician (over 1500 papers!) who worked in graph theory and combinatorics. The Erdös number was how many papers it took by coauthoring to connect you to Erdös. He was also wonderfully eccentric. Once, visiting a friend, he woke in the night to get some juice. In the morning, his friend found red liquid all over the floor. Erdös, puzzled by the juice carton, had simply stabbed a hole in the side to drink from. His biography is a fascinating glimpse into a nearly alien mind.

In my own research, I look at how oscillators synchronize in small networks, such as rings. Even in a simple ring, many new types of synchrony occur, compared to all-to-all connections. It is easy to believe that the structure of the brain, and how various regions and subregions connect, might greatly influence human thinking. On a more science fiction note, I suspect that artificial intelligence will not exist in machines without complex networks of elements.

This was just a very quick overview of a huge field. In the future, I plan to write on topics like small-world networks, scale-free networks, and synchrony on networks. Check out my other science posts on synchrony, fractals, the Mandelbrot set, and chaos.

The Beautiful Lab

Leave a reply

Across the country, thousands of labs study thousands of topics. In my lab, we study nonlinear dynamics in electrochemical oscillators. The dynamics of these oscillators can be used to make math models for other oscillators we might be very interested in, like heart cells, breathing, and neurons in the brain. Oscillators and their dynamics show up in many places. In a previous post on synchrony, I discuss some of these dynamics.

My experiments aren’t particularly much to look at. The beauty in mostly in the data. But here are a few of my better snaps over the years. There can also be science in the photographic technique. The bottom two photos were taken using reverse lens macro, a cheap way to do great zoom shots.

From top to bottom the photos below show: the electrochemical 3 electrode cell, the variable resistance resistors for each electrode, and a capacitor. The featured image is of some resistors.

SONY DSC

SONY DSC SONY DSC

Fun Science: Astronomical

Leave a reply

I first became interested in science when my brother told me there was a black hole under his bed (this was a ploy to prevent me from snooping there– this is how nerd children fight). Once I could read, I wanted to know if this could be possible; one should be skeptical of information provided by siblings. Frustratingly, none of the books I read discussed if an event horizon could be put under a bed. Pretty shoddy science. There was much discussion of micro-blackholes, with some description of their size. But what the heck was a nanometer? Bigger or smaller than a bed?

Even now, the scales of the universe boggle my mind. A human is so small. The diameter of the Earth (a small planet), is roughly 7 million times the height of a typical person. If you lined up every person in the state of Virginia head to toe, you would roughly approximate the Earth’s diameter. The diameter of the Sun is 100 times bigger (two orders of magnitude) than the Earth. If you lined up every person in the United States head to toe, you’d only get to half of the Sun’s diameter. The red giant Betelgeuse (the reddish star that is Orion’s left shoulder) is 700 times bigger than the sun.

The solar system is bigger yet–Neptune is 30 times as far from the Sun as Earth, at about 3200 times the radius of the Sun. It takes light 4 hours to reach Neptune. The Oort cloud, the farthest reach of our solar system and the hypothesized source of most comets, is a light year from the Sun.

From Wikipedia

Our solar system sits on one branch of the Milky Way, which is a galaxy 100,000 light years across (7×1011 times the diameter of the Sun–a meter is roughly 1012 times as big as a hydrogen atom). Our galaxy is 2.5 million light years from the nearest galaxy, Andromeda. Our galaxy is one of more than 50 galaxies in the Local Group. This piece of the universe is about 10 million light years in size. Wikipedia suggests there may be 100 billion galaxies in the universe. We have observed as far as 47 billion light years away, but the universe might be bigger (more intimidating statistics here).

And all of these things are slowly interacting. With all that, how could we not write science fiction?

Fractals in Life: photos

1 Reply

Fractals are a branch of math that better describes nature. Before fractals, there was Euclidean geometry, the geometry of lines, planes, and spaces. Euclidean geometry cannot give the length of a rough coastline; neither can it give the surface area of shaggy tree bark. The answer you arrive at in Euclidean geometry depends upon the scale at which you examine an object– intuitively the distance an ant travels over rough terrain is different from the distance we cover walking. The ant interacts with the terrain at a different length scale than we do. Fractal geometry is designed to handle objects with multiple meaningful length scales.

Fractal objects are sometimes called “scale-free“. This means that the object looks roughly the same even if examined at very different zooms. Many natural objects look similar at multiple zooms. Below, I include a few. The craters on the moon are scale-free. If you keep zooming in, you could not tell the scale of the image.

frac (1)

Terrain is often scale-free in appearance– a few years ago there was a joke photo with a penny for scale. The owners of the photo subsequently revealed that the “penny” was actually 3 feet across. I couldn’t find the photo, but you cannot tell the difference. The reveal was startling. Below is a picture of Mount St Helens. The top of this mountain is five miles (3.2ish km) away. Streams carry silt away from the mountain, as you can see more towards the foreground. They look like tiny streams. These are full-sized rivers. Mount St. Helens lacks much of the vegetation and features we would usually use to determine scale. The result is amazingly disorienting, and demonstrates scale invariance.

SONY DSC

Plants are often scale free too. Small branches are very similar in appearance to large branches. Ferns look very fractal. Below is a picture of Huperzia phlegmaria. Each time this plant branches, there are exactly two branches. Along its length, it branches many times. It is a physical realization of a binary tree.

SONY DSC

For more about fractals, read my posts about fractal measurement and the mandelbrot set.